MLP(Multi-Layer Perceptron)

- Percetron은 알고리즘의 이름이다.

- 다수의 입력 -> 하나의 출력

 

- 입력층, 은닉층, 출력층으로 구성되어 있다. 

- MLP는 일반적으로 최소 하나 이상의 비선형 은닉 계층이 포함되며, 이러한 계층은 학습 데이터에서 복잡한 패턴을 추출하는 데 도움이 된다.

 

- 각 입력 x에 대응되는 weight(w), 1개의 노드에 입력되는 bias(b) 존재한다.

- 가중합으로 이루어진 결과치에 활성화 함수(h) 적용

 

 

- 각 층별로 모든 노드가 연결되어 weight를 가지는 계층을 FC layer라고 함

 

 

 

활성화 함수

- 입력값들의 가중합을 통해 노드의 활성화 여부를 판단하는 함수

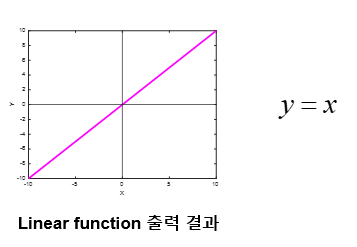
• linear function

  - 입력 값을 그대로 출력으로 내보내는 함수

  - Regression(회귀) 문제의 출력층에서 주로 사용됨

• Step function

  - 0 이하면 0, 0보다 크면 1을 출력

  - 역전파를 통한 학습 불가능 (미분 불가)

  - 이진분류시 출력층에서 사용하기 적합함

• Sigmoid function

  - 0~1 사이 실수를 출력 -> 확률로 해석 가능

  - 기울기가 발생하지 않는 지점이 존재함

  - exp 연산의 속도가 느림

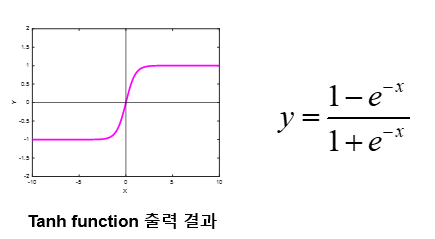
• Hypergolic tangent(tanh) function

  -  -1 ~ 1 사이 실수를 출력

  - Sigmoid 함수보다 출력의 범위가 큼

  - Sigmoid 함수보다 최대 기울기가 큼

• Rectified Linear Unit(ReLU) function

   - 0 이하일 때 0, 0 보다 크면 값을 그대로 출력

   - 단순한 연산으로 학습 속다가 빠름

   - 입력 값이 0 이하인 경우 기울기는 항상 0

• Leaky ReLU function

   - 0 이하일 때 0.1을 곱한 값이 출력됨

   - ReLU 함수의 음수 구간 기울기 소실 문제를 보완함

• Parametric ReLU(PReLU) function

   - Leaky ReLU와 유사

   - 음수 구간 기울기를 결정하는 p는 학습 가능한 파라미터

 

• Sofymax function

   - 여러 개의 입력을 받아 각각의 확률 값으로 출력

   - 0~1 사이 실수를 출력하고, 모든 출력의 합은 1 (확률로 해석)

   - Multi-label classification 모델의 출력층에 주로 사용

 

 

 

 

 

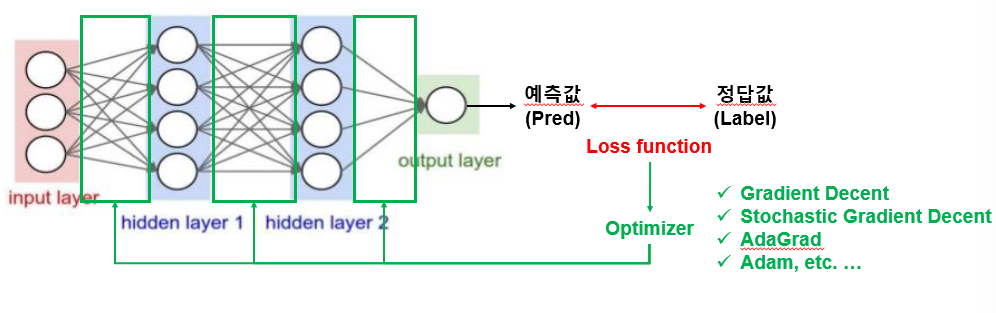
Loss Function

: 학습 모델이 얼마나 잘못 예측하고 있는지를 표현하는 지표

: 예측값과 실제 값의 차이를 Loss라고 함. 이 Loss를 줄이는 방향으로 학습이 진행

-> 값이 낮을수록 모델이 정확하게 예측했다고 해석할 수 있음

 

 

 

Optimization

: Loss function을 최소로 만들기 위한 가중치, 편향을 찾는 알고리즘이다.

: Learning rate: 가중치를 얼마나 변경시킬지 정하는 상수

 

 

 

Batch size

: 한 번에 학습할 데이터의 개수

1 Epoch

: 전체 데이터셋에 대해 1회 학습

1 lteration

: 1개의 batch에 대해 학습